PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning
Por um escritor misterioso
Descrição
It is shown that the CG method with variable preconditioning under this assumption may not give improvement, compared to the steepest descent (SD) method, and a new elegant geometric proof of the SD convergence rate bound is given. We analyze the conjugate gradient (CG) method with variable preconditioning for solving a linear system with a real symmetric positive definite (SPD) matrix of coefficients $A$. We assume that the preconditioner is SPD on each step, and that the condition number of the preconditioned system matrix is bounded above by a constant independent of the step number. We show that the CG method with variable preconditioning under this assumption may not give improvement, compared to the steepest descent (SD) method. We describe the basic theory of CG methods with variable preconditioning with the emphasis on “worst case” scenarios, and provide complete proofs of all facts not available in the literature. We give a new elegant geometric proof of the SD convergence rate bound. Our numerical experiments, comparing the preconditioned SD and CG methods, not only support and illustrate our theoretical findings, but also reveal two surprising and potentially practically important effects. First, we analyze variable preconditioning in the form of inner-outer iterations. In previous such tests, the unpreconditioned CG inner iterations are applied to an artificial system with some fixed preconditioner as a matrix of coefficients. We test a different scenario, where the unpreconditioned CG inner iterations solve linear systems with the original system matrix $A$. We demonstrate that the CG-SD inner-outer iterations perform as well as the CG-CG inner-outer iterations in these tests. Second, we compare the CG methods using a two-grid preconditioning with fixed and randomly chosen coarse grids, and observe that the fixed preconditioner method is twice as slow as the method with random preconditioning.
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://indrag49.github.io/Numerical-Optimization/bookdownproj_files/figure-html/unnamed-chunk-10-1.png)
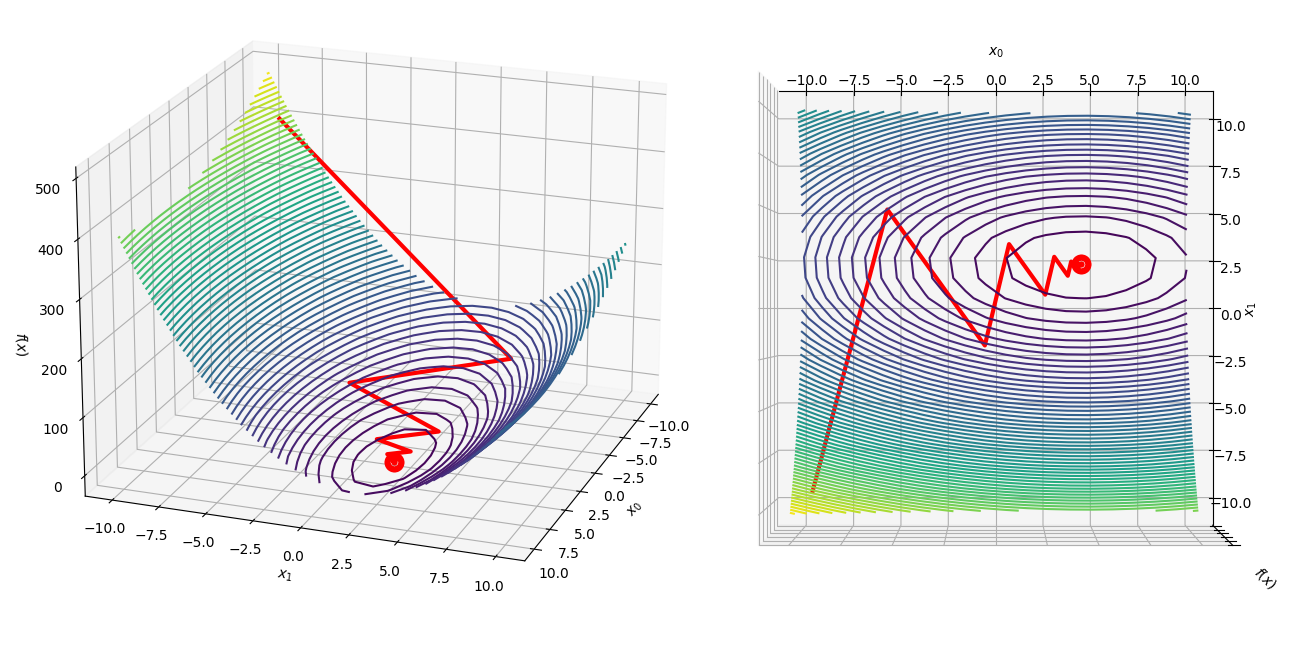
Chapter 5 Conjugate Gradient Methods
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://d3i71xaburhd42.cloudfront.net/70000f7791ab8519429ce939bc897738a05939c3/26-Figure19-1.png)
PDF] An Introduction to the Conjugate Gradient Method Without the
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://media.springernature.com/m685/springer-static/image/art%3A10.1007%2Fs11590-022-01867-9/MediaObjects/11590_2022_1867_Figa_HTML.png)
A link between the steepest descent method and fixed-point
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://media.springernature.com/lw685/springer-static/image/chp%3A10.1007%2F978-3-031-08720-2_3/MediaObjects/527858_1_En_3_Fig2_HTML.png)
Steepest Descent Methods
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://i1.rgstatic.net/publication/220493430_Algorithm_809_PREQN_Fortran_77_subroutines_for_preconditioning_the_conjugate_gradient_method/links/546ec9920cf2b5fc17607f32/largepreview.png)
PDF) Algorithm 809: PREQN: Fortran 77 subroutines for
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://www.mdpi.com/mathematics/mathematics-11-02466/article_deploy/html/images/mathematics-11-02466-g001.png)
Mathematics, Free Full-Text
Two Algorithms Related to the Method of Steepest Descent
Hyperbolic Pairs in the Method of Conjugate Gradients
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://0.academia-photos.com/attachment_thumbnails/59852465/mini_magick20190624-19559-1t5imq9.png?1561401861)
PDF) A New Extended PR Conjugate Gradient Method for Solving
de
por adulto (o preço varia de acordo com o tamanho do grupo)