Rooks Problem -- from Wolfram MathWorld
Por um escritor misterioso
Descrição
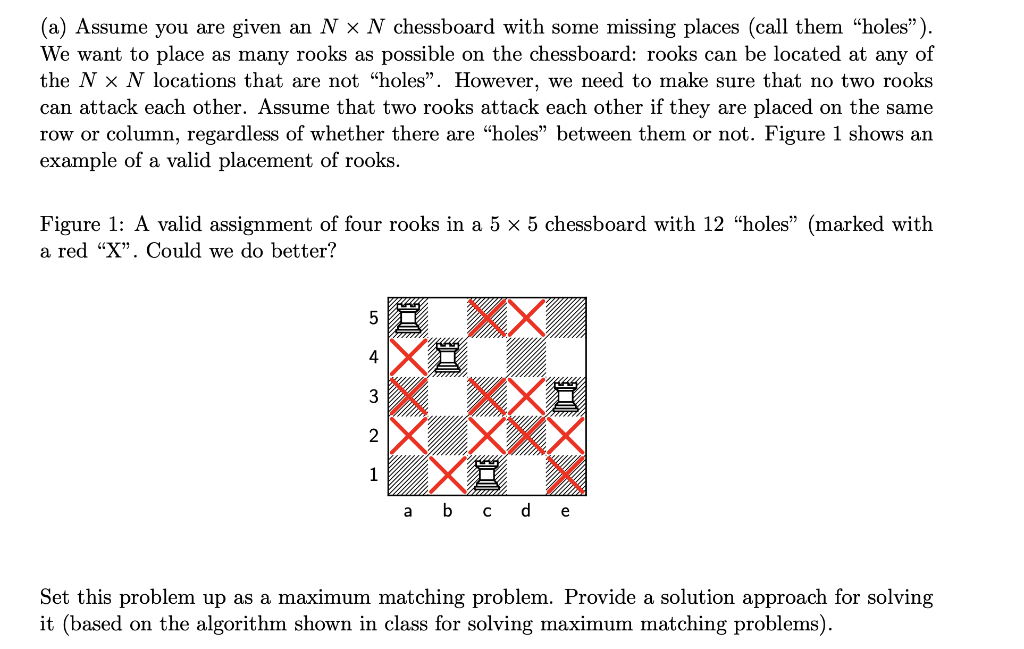
The rook is a chess piece that may move any number of spaces either horizontally or vertically per move. The maximum number of nonattacking rooks that may be placed on an n×n chessboard is n. This arrangement is achieved by placing the rooks along the diagonal (Madachy 1979). The total number of ways of placing n nonattacking rooks on an n×n board is n! (Madachy 1979, p. 47). In general, the polynomial R_(mn)(x)=sum_(k)r_k^((m,n))x^k whose coefficients r_k^((m,n)) give the
An Archetype Theory of Puzzles

Typographic Playing Cards: Mathematical Playing Cards by Wolfram Research, Inc.

Stella Octangula Stella, Introduction to geometry, Polyhedron

Solved Permutations This method determines if one int array
How many ways are there to place two identical rooks on a standard 8x8 checkerboard so that they are attacking each other? - Quora
What is the minimum number of Queens with which you can cover every square of chess board? Also show their arrangement. - Quora
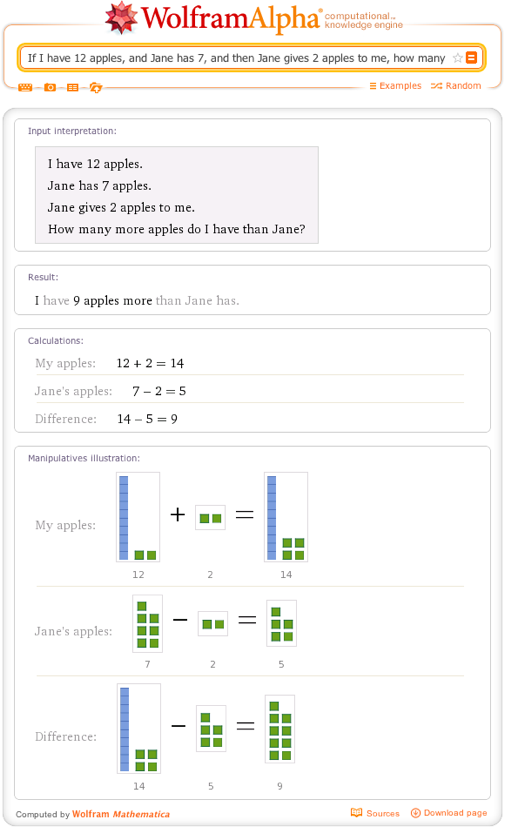
Solving Word Problems with Wolfram, Alpha—Wolfram

Chained permutations and alternating sign matrices—Inspired by three-person chess - ScienceDirect

Computing the Wronskian with WolframAlpha.com
de
por adulto (o preço varia de acordo com o tamanho do grupo)